

後輩から以下のようなLINEが来ました。
「適切」という言葉が曖昧ですが、以下のように解釈しました。
平易な言葉でいうと、なるべく少ない材料で、使いまわせるように、余りは出来る限り長く取ろうという意味です。
目次
Rubyで総当りのプログラムを作りました。後述の通り、計算量は大きいですが、ひとまず動くので問題ないと思います。
# 材料の長さ(今回は6000mm)
L = 6000
# 必要な長さと本数
# ここでは、1322mmを2本、1264mmを6本、1283mmを6本
needs = {
a: {length: 1322, num: 2},
b: {length: 1264, num: 6},
c: {length: 1283, num: 6}
}
def culc(require_list)
sums = []
require_list.each do |k, v|
v[:num].times do |i|
# 配列をコピーして、キーを追加
added_sums = Marshal.load(Marshal.dump(sums))
added_sums.map{|el| el << k }
# もとの配列とキーを追加した配列を結合
sums.concat added_sums
# キー単体を追加
sums << [k]
# 定尺を超えた物を削除
sums.delete_if{|x| x.inject(0) {|sum, n| sum + require_list[n][:length]} > L}
# 重複を削除
sums.uniq!
end
end
hashes = []
sums.each do |nl|
hashes << {pattern: nl, score: nl.inject(0) {|sum,n| sum + require_list[n][:length]}}
end
max_pattern = hashes.max{|a,b| a[:score] <=> b[:score]}
p max_pattern
max_pattern[:pattern].each do |item|
require_list[item][:num] -= 1
end
require_list.delete_if{|k, v| v[:num] <= 0}
if require_list.size > 0
culc require_list
end
end
puts "required list"
puts "====================================="
p needs
puts ""
puts "best combination"
puts "====================================="
culc needs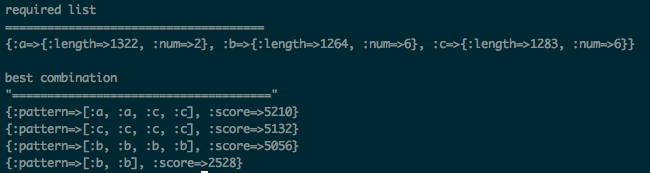
これはカットストック問題と呼ばれるNP困難な問題として知られています。
今回は小さい数でやったため、上手く結果が出力されていましたが、大きな数になると途端に計算量が増えてしまい、結果を出すことが難しくなってしまいます。
少し材を切り出したいときぐらいには、実用に耐えうると思います。
必要に迫られて、プログラムで解決するのは楽しいので、身近な問題に是非チャレンジしてみてください。